
and the area of its base = area of the regular hexagon Then, the area of side-faces of the prism Solution: Let a be the length of a side of the regular hexagon. If the area of the whole surface of the prism be 1152√3 sq.cm. stands on a base which is a regular ,hexagon. Now, the volume of the prism = area of the base × height.Īgain, area of lateral surface of the prism = perimeter of the base × height of the prism Then, the area of base of the prism = area of the regular pentagon of side a. Solution: Let a be the length of a side of the regular pentagon. If its height, volume and the area of lateral surface be h v and s respectively, prove that,ĢOvh = s²cot 36°. The base of a right prism Is a regular pentagon. Therefore, the required height of the prism = 8√3cm. Or, 576√3 = perimeter of the base × height of the prism + 2 × 96√3 = area of its lateral faces + 2 × area of its base Now, the area of the whole surface of the prism. , the area of the base of the prism = 96√3 sq. Where a is the length of the side of a polygon. Solution: We know that the area of a regular polygon of n sides is (na²/4) cot (π/n). If the of the whole surface of the prism is 576√3 sq. The base of a right prism is a regular hexagon of side 8 cm. Therefore the required height of the prism is 15 inches.Īgain, the area of the lateral surface of the prismģ. Then, volume of the prism = area of its base × its height. Let h be the required height of the right prism.

= 1/2 × (sum of the lengths of the parallel sides) × (distance between the parallel sides) Now, from the right - angled CEB we get, Solution: Let the base of the right prism be the trapezium ABCD whose parallel sides are AB and DC and the third side DA is perpendicular to both AB and DC.ĭraw CE perpendicular to AB. If the third side of the trapezium be perpendicular to the parallel sides and is of length 8 inches, find the height of the prism and the area of its lateral surface.
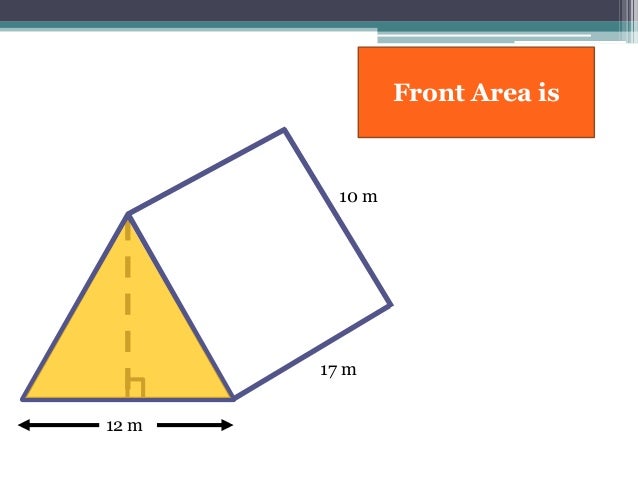
inches and its base trapezium whose parallel sides are of lengths 8 inches and I 4 inches. Therefore, the area of total lateral surface of the prismĢ. The volume of a right prism is 1320 cu. Solution: Let s be the semi-perimeter of the triangular base of the prism. find the area of total lateral surface, area of the whole surface and the volume of the prism. The base of a right prism is a triangle whose sides arc of lengths 13 cm., 20 cm. (iii) volume of a right prism = ( area of base ) × (height).ġ. = area of its side faces + 2 × area of its base (ii) area of total surfaces of a right prism (i) area of the side faces (i.e., lateral surfaces) of a right prism If h be the height (i.e., the perpendicular distance between the parallel end faces) and the lengths of the sides of the base polygon be a, b, c, d. Right Prism: If the side-edges of a prism are perpendicular to its ends (or to base), it is called a right prism otherwise, a prism is said to be oblique.įor a right prism the side faces are all rectangles and each side-edge is equal its height. The perpendicular distance between two ends of a prism is called its height. ABCDE is the base of the prism given in the figure. The end on which a prism stands, is called its base. These side-edges are all parallel and equal in length. The straight line along which two adjacent side faces of a prism intersect is called a side-edge of the prism.
In particular, a prism is said to be triangular if its two ends are triangles it is called quadrangular if its ends are quadrilaterals and so on. A prism is said to be polygonal if its two ends are polygons. The number of such side faces is equal to the number of the sides of the polygon at the ends of the prism. are its side faces and these faces are parallelograms. The figure below shows the two kinds of triangular prisms.A prism has been displayed in the given figure ABCDE and PQRST are its two ends these two are congruent parallel planes.
Given below are the main characteristics of a Triangular prism.


 0 kommentar(er)
0 kommentar(er)
